「人口論」と「人月の神話」からみる総生産曲線
前回のブログで、時代も立場も異なる、2つの著書に見る、
共通性を通じて、問題提起を行いました。
- ロバート・マルサスの「人口論」
- フレデリック・ブルックス,Jrの「人月の神話」
マルサスは、19世紀のイギリスの経済学者で、
ブルックス,Jrは、20世紀のアメリカのソフトウェア技術者です。
そこで、当ブログで、いつも行っている、「グラフ式思考法」で考えてみましょう。
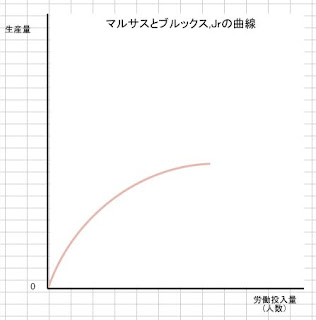
すると、以下のような、総生産曲線が出来上がります。
マルサスとブルックスJrの曲線
このグラフをよく観察すると、以下のような特徴が、挙げられます。
- 労働投入量が少ないときは、傾きが大きい
- 労働投入量が多いときは、傾きが小さい
つまり、労働投入量が変化するに従って、生産量の増加が鈍っているように見えます。
マルサスとブルックスの曲線の特徴(曲線の接線の特徴)
「微分」を思い出してみよう!
労働投入量が、追加的に変化しているときに、
生産量の増加率が、どれぐらい変化しているかを、分析するためには、
微分の概念が、非常に有効です。
Tractor / ototadana
ここでいう微分とは、dx/dyや⊿yなど記号を使った、計算式を展開することではありません。
単に「変化率を測る」ぐらいの、意味に置き換えてくだされば、結構です。
(微分に関する詳しいブログは、コチラ)
その「変化率」をグラフにして表すと、次のような右下がりのグラフになります。
これを、限界生産物曲線と言います。
限界生産物曲線
「数字」にして書き出してみよう!
先にあげた総生産曲線と、限界生産物曲線の、2種類のグラフが、
今回のテーマである、「限界収穫逓減の法則」のミソになります。
ブルックス,Jrのように、ソフトウェア開発における、プログラムコードを使った、
数値の例を用いて、限界生産曲線とは、どんな現象なのかを、確認してみましょう。
プログラムコードの総生成量と限界生成量
労働投入量、つまり、プログラマーを増やすに従って、
プログラムコードの総量は、確かに増加していますが、その増加量は、次第に鈍っています。
4bit computer / torisan3500
この現象を、ミクロ経済学的に説明をすると、
「もう1単位の労働を追加したときの限界生産物は減少している」、という説明になります。
ここでいう限界とは、「追加的な」という意味に置き換えてください。
二重的な修飾で、日本語としてちょっとおかしい気もしますが、
経済学では、こういう言い方をするようです。
(つづく)